Grundlagen der photothermischen Schichtdickenmessung
- September 15, 2020

Photothermische Messungen sind zur berührungslosen Schichtdickenmessung von Lacken auf Metallen, Kunststoffen und anderen Materialien geeignet. In dieser Application Note stellen wir das Messprinzip vor und informieren über die Voraussetzungen für photothermische Schichtdickenmessungen.
Einführung in die photothermische Schichtdickenmessung
In nahezu allen industriellen Bereichen werden Bauteile beschichtet. Es handelt sich z.B. um Korrosionsschutz, Farblackierungen, Pulverlacke, Klarlacke oder
funktionelle Oberflächenbeschichtungen. Für die Qualitäts- und Prozesskontrolle ist es von größter Bedeutung, die Dicke der aufgetragenen Schicht messen zu können.
Übliche Verfahren hierfür sind beispielsweise Wirbelstrom- oder induktive Messverfahren, diese benötigen aber metallische oder sogar speziell ferromagnetische Substrate. Andere Verfahren, wie z.B. Ultraschall, benötigen direkten Kontakt zur Probe und sind daher für Messungen auf noch nassen Beschichtungen oder nicht eingebrannten Pulverlacken ungeeignet.
Die photothermische Schichtdickenmesstechnik ist eine optische Messtechnik, die prinzipbedingt auf allen Substratmaterialien funktioniert und berührungslos arbeitet. Es wird bei dieser Methode die thermooptische Interferenz ausgenutzt, um die Dicke z.B. einer Lackschicht zu messen. Dieses Verfahren soll im Folgenden näher vorgestellt und die Voraussetzungen für eine erfolgreiche Messung dargelegt werden.
Das Messprinzip
Der photothermische Effekt
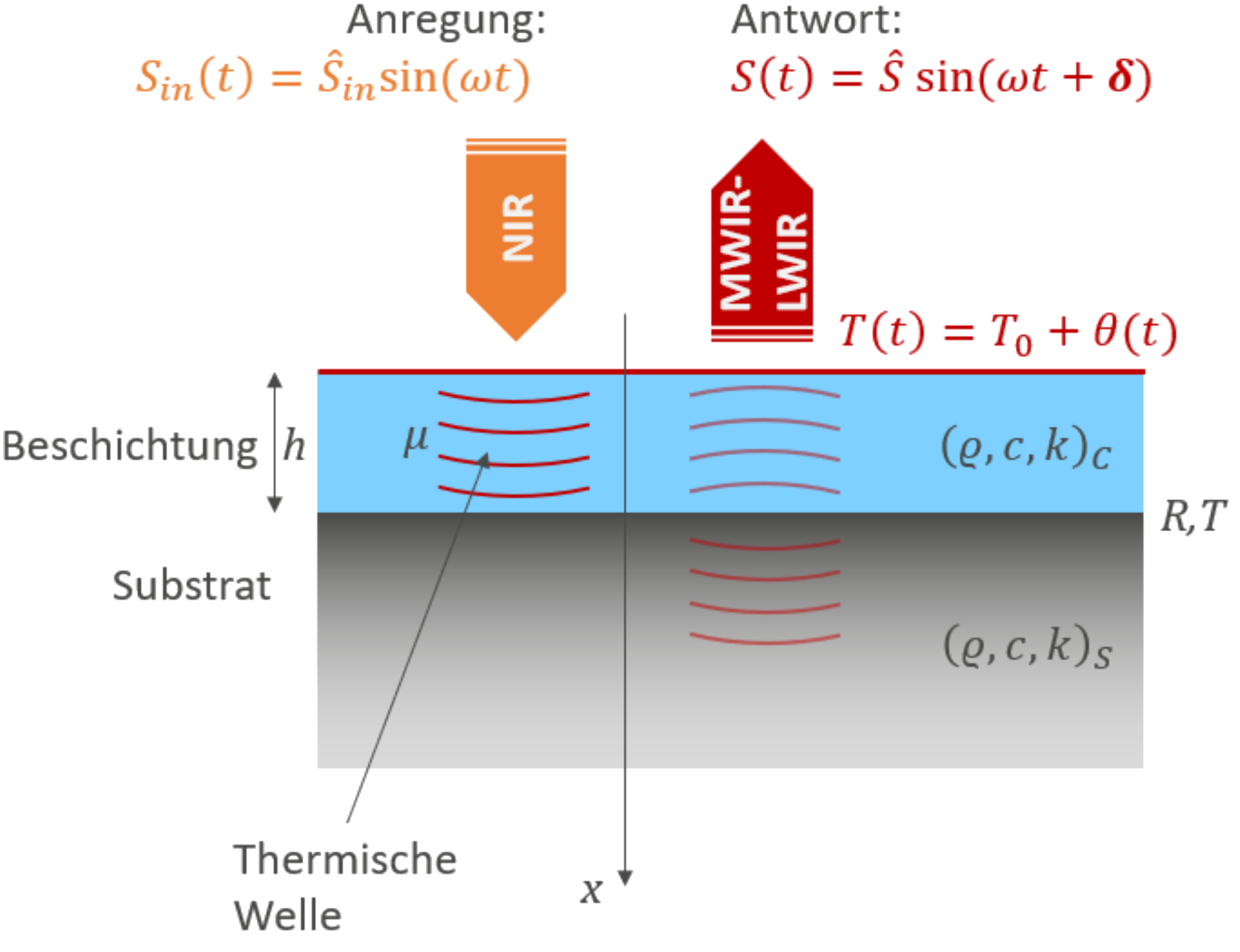
Abb. 1: Überblick zum photothermischen Effekt und zur Anregung thermischer Wellen. Betrachtet wird ein typisches System aus einem Substrat, das mit einer Beschichtung der Schichtdicke h versehen ist.
Der photothermische Effekt ist ein Phänomen, das seit ca. 1880 bekannt ist. Er bezeichnet den Effekt, dass Materialien optische Strahlung absorbieren können und in Wärme umwandeln [1]. Diesen Effekt nutzte schon Bell bei der Konstruktion seines „Photophons“.
Wie ausgeprägt dieser Effekt ist, hängt vom Beschichtungsmaterial ab: Materialien, die optische Strahlung nur schwach absorbieren, zeigen nur geringe Temperaturänderungen, ebenso Materialien, deren Oberflächen stark reflektieren (vgl. Abs. „Einflüsse der Probe“). Materialien mit glänzender Oberfläche und/oder transparenter Erscheinung erwärmen sich daher weniger stark als zum Beispiel matte und/oder intransparente Materialien.
Im dargestellten Fall wird zur thermischen Anregung Licht aus dem nahinfraroten Teil des optischen Spektrums (NIR) verwendet. Die Beschichtung wandelt die absorbierte Energie in Wärme um, was zu einer Temperaturänderung t führt. Dabei wird Schwarzkörperstrahlung ausgesendet, deren Wellenlänge im mittleren bis langwelligen Infrarotbereich (MWIR-LWIR) liegt. Das Beschichtungsmaterial ist charakterisiert durch seine spezifische Dichte , Wärmekapazität c und Wärmeleitkoeffizient k.
Thermische Wellen
Thermische Wellen sind in der Physik lange bekannt. Moduliert man die Intensität der anregenden Strahlung, wird in der Beschichtung eine thermische Welle angeregt. Thermische Wellen entstehen aus der Lösung der eindimensionalen Wärmeleitungsgleichung.
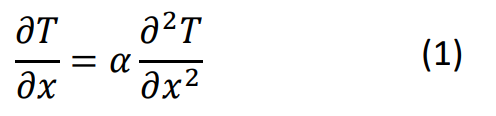
mit der thermischen Diffusivität α = k/ϱc, wenn als Randbedingung ein, wie dargestellt, zeitlich modulierter Wärmestrom vorgegeben wird [2]. Die Erwärmung des Materials ist dann ebenfalls moduliert und beschreibt eine in positiver Richtung laufende Welle.
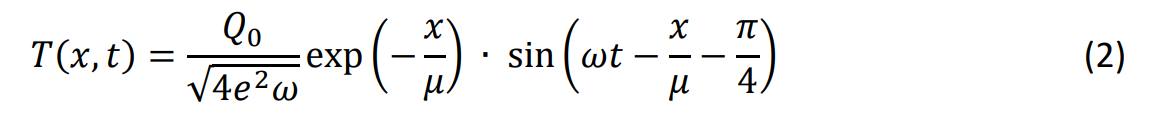
Hierin ist mit e = ϱck die thermische Effusivität bezeichnet. Der Phasenunterschied -π/4 entsteht durch die Vorgabe eines Wärmestroms.
Thermische Wellen werden durch die thermische Wellenlänge μ = 2α/ω beschrieben. Die Wellenlänge der thermischen Welle lässt sich also durch die Modulationsfrequenz beeinflussen: Je geringer die Modulationsfrequenz, desto größer die Eindringtiefe.
Zum ersten Mal zu Messzwecken wurden thermische Wellen im Rahmen der photoakustischen Spektroskopie innerhalb der Materialcharakterisierung angewendet. Hierbei wurde die thermische Expansion eines Gases in einem abgeschlossenen Volumen mittels eines Mikrofons aufgezeichnet und mit der Anregung korreliert [3,4].
Thermooptik und thermische Interferenz
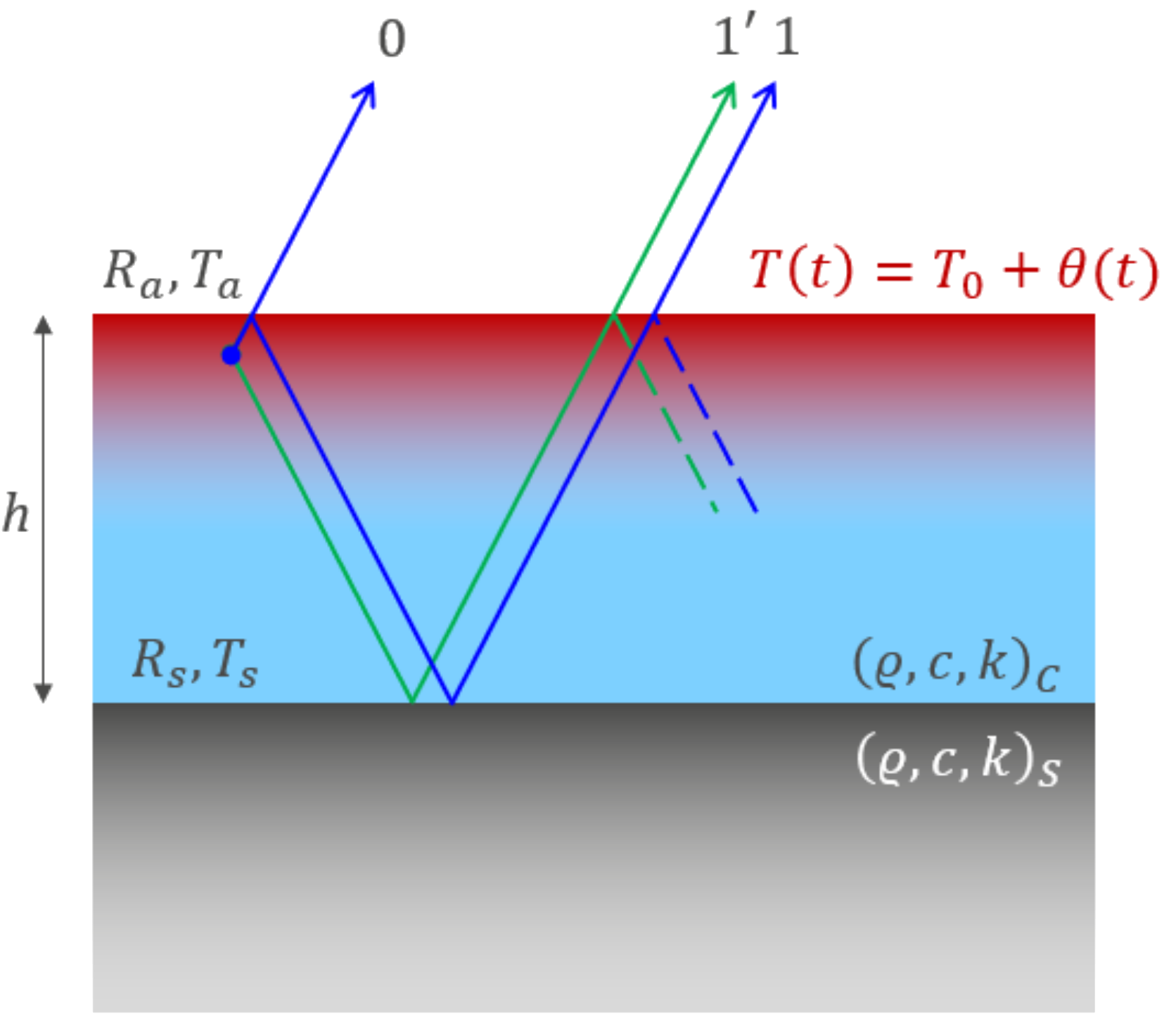
Abb. 2: Thermische Interferenz in einer Probe. Hier wurde die Beschichtung aus Gründen der Prägnanz übertrieben dick gezeichnet, auch die Erwärmungszone ist übertrieben ausgedehnt gezeichnet. Erklärungen sind im Text gegeben. |
Thermische Wellen verhalten sich in vielerlei Hinsicht wie mechanische, akustische und optische Wellen. Basierend auf den Effusivitäten von Beschichtung eC und Substrat eS lässt sich ein thermooptischer Brechungsindex
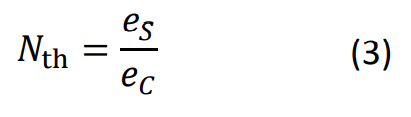
definieren, der den reflektierten und den transmittierten Wellenanteil beschreibt:
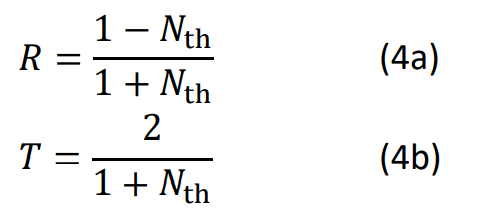
Wenn die Effusivitäten von Beschichtung und Substrat ungefähr gleich sind, ist der thermische Brechungsindex und damit das Reflektionsvermögen der Grenzfläche gering. Messungen sind dann nicht oder nur schwer möglich. In der Praxis ist dies sehr selten zu beobachten. Dem kann z.B. begegnet werden, indem die Beschichtung bzw. der Lack im nassen Zustand inline gemessen wird.
Bei der photothermischen Schichtdickenmessung wird ausgenutzt, dass thermische Wellen in dünnen Schichten Interferenzeffekte zeigen. Dieser Effekt wird in Abb. 2 beschrieben. Trifft anregende Strahlung auf die Oberfläche eines gut absorbierenden Materials, so werden im oberflächennahen Bereich thermische Wellen angeregt. Von einem Anregungszentrum gehen zwei Wellenzüge ab: einer, der zunächst an der Grenzfläche zur Atmosphäre reflektiert wird und einer, der zunächst an der Grenzfläche zum Substrat reflektiert wird. Bei Überlagerung beider Wellenzüge entsteht eine resultierende thermische Welle, die gegenüber der anregenden Strahlung einen Phasenunterschied aufweist:
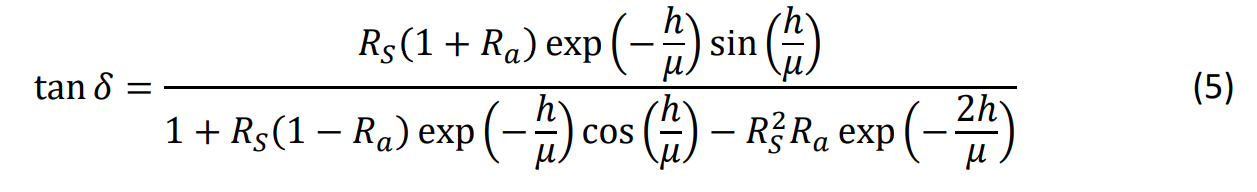
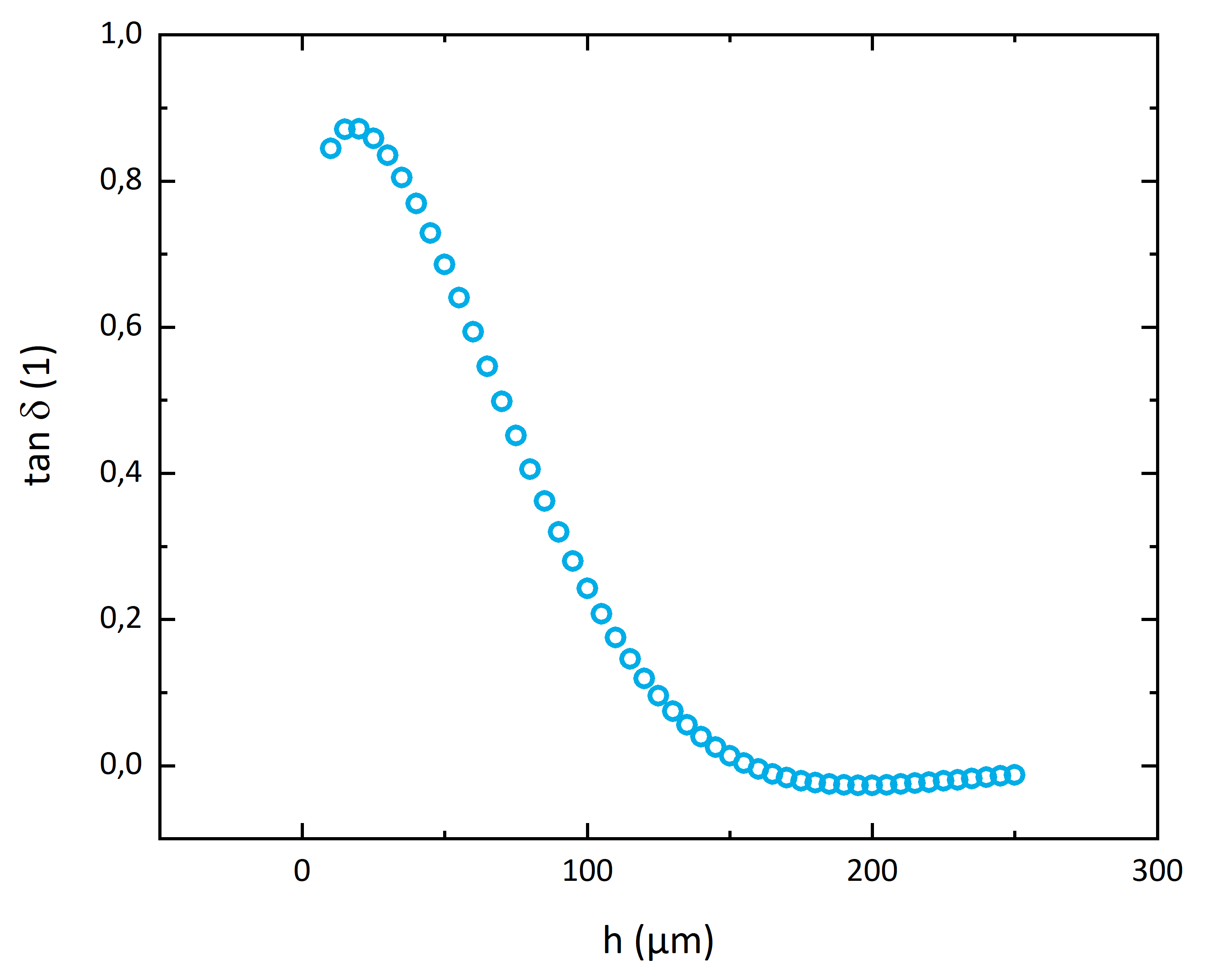
Abb. 3: Abhängigkeit des Phasenfaktors tan δ von der Schichtdicke h, hier exemplarisch gerechnet für lackiertes Aluminium.
Abbildung 3 zeigt exemplarisch den Verlauf des Phasenfaktors tan δ in Abhängigkeit von der Schichtdicke h. Der Phasenunterschied hängt neben den thermooptischen Parametern
von der Schichtdicke h ab. Bei Kenntnis der thermooptischen Parameter kann also ein bekannter Gangunterschied in eine Schichtdicke umgerechnet werden. Diese Gangunterschiede lassen sich etwa durch Lock-In-Verfahren oder Fourieranalyse sehr präzise bestimmen.
Einflüsse der Probe
Emissionsgrad und Oberflächenreflexion
Der Emissionsgrad (Emissivität) ist eine dimensionslose Größe, die beschreibt, wie stark eine Oberfläche Strahlung emittiert [5]. Ein schwarzer Strahler besitzt einen Emissionsgrad ϵ = 1, ein grauer Strahler besitzt einen Emissionsgrad ϵ < 1, ein nichtgrauer Strahler besitzt einen wellenlängenabhängigen
Emissionsgrad ϵ = ϵ < 1. Der Emissionsgrad beeinflusst direkt die Intensität der abgegebenen Strahlung nach dem Stefan-Boltzmann-Gesetz (Stefan-Boltzmann-Konstante σ = 5,67 ∙ 10-8 Wm-2K-4):
![]()
Einen größeren Einfluss auf die photothermische Messung besitzt dagegen der optische Reflexionsgrad (Reflexionsvermögen) der Oberfläche für das anregende Licht. Der Reflexionsgrad Ropt bestimmt, wie stark die Oberfläche erwärmt wird (vgl. Gln. (7a,b)). Schwarze Oberflächen besitzen einen geringen Reflexionsgrad von weniger als 0,1 und helle Oberflächen einen hohen Reflexionsgrad von über 0,9. Der Emissionsgrad der meisten Nichtmetalle, Lacke, Farben und Kunststoffe liegt im Infrarotbereich über 0,9 und ist weitgehend wellenlängenunabhängig. Diese Materialien sind in der Regel mit IR-Detektoren gut zu messen.
Der Einfluss des Reflexionsvermögens lässt sich gut durch Messung der Temperaturänderung nachweisen, die durch Bestrahlung mit Infrarotlicht (NIR) bei verschiedenen Oberflächenfärbungen hervorgerufen wird.
Wie in Abb. 4 exemplarisch gezeigt, weichen die Signalamplituden der Materialien mit unterschiedlichem Reflexionsgrad um 1-2 Größenordnungen voneinander ab. Ein Vergleich der Amplituden führt auf einen Reflexionsgrad von etwa 0,05 für Gummi und 0,96 für rotes Papier und 0,99 für weißes Papier. Entsprechend gering ist die Temperaturänderung bei den Papierproben. Ist für eine Messanwendung die Erwärmung aufgrund des hohen Reflexionsgrads zu gering, sollte eine Strahlquelle eingesetzt werden, deren Wellenlänge die weniger stark reflektiert wird.
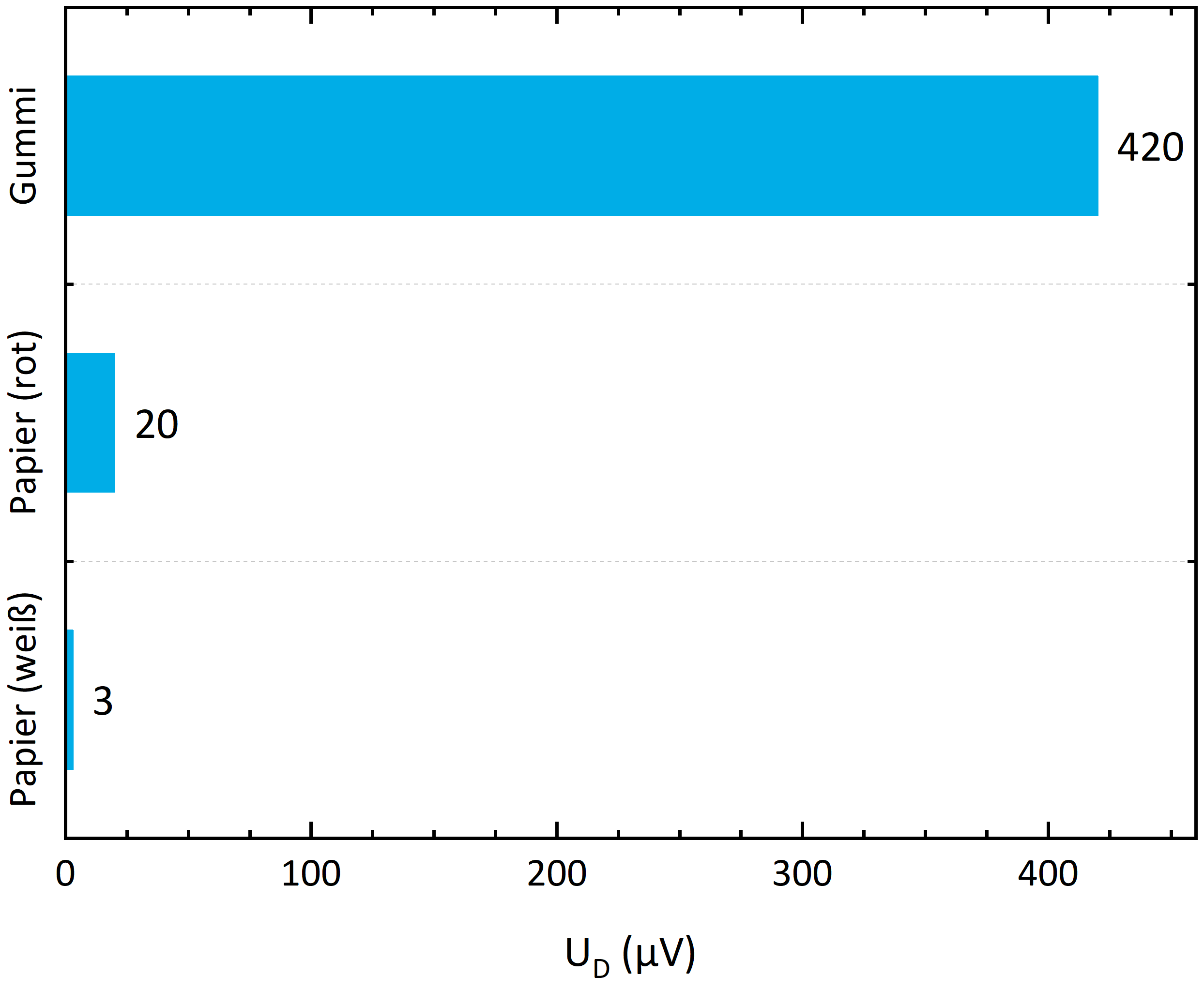
| Abb. 4: Amplitude der Detektorspannung für verschiedenfarbige Oberflächen. |
Optische Absorption
Weiteren Einfluss auf die Messung hat der Absorptionskoeffizient Ropt. Dieser ist der Kehrwert der Eindringtiefe der optischen Strahlung in das Material. Die Erwärmung der Probe und damit das für Messungen zur Verfügung stehende Antwortsignal ist umso stärker, je größer der Absorptionskoeffizient ist. Der Absorptionskoeffizient reicht von etwa 106 – 107 m-1 für intransparente Materialien bis nahe 0 für transparente Materialien.
Nach [1] wirkt sich der Absorptionskoeffizient auch auf die Ausdehnung der Entstehungszone thermischer Wellen aus. Diese wurde im Abschnitt „Thermooptik und thermische Interferenz“ noch als oberflächennah und klein im Vergleich zur Schichtdicke angenommen. Für die Temperaturänderung θ0 gilt in diesem Fall, wie an gleicher Stelle hergeleitet:
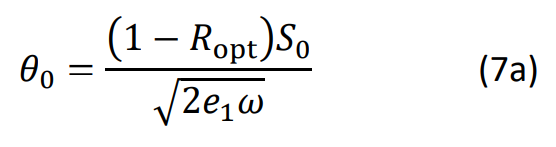
im Fall schwacher optischer Absorption gilt dagegen:
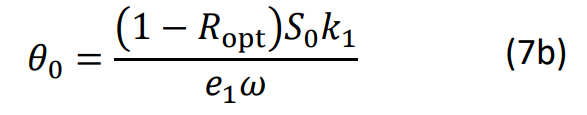
Im ersten Fall fällt die Temperaturamplitude also proportional mit der Wurzel der Modulationsfrequenz, im zweiten Fall dagegen proportional mit der Modulationsfrequenz selbst. In beiden Gleichungen bezeichnet S0 die Intensität der anregenden Strahlung. Im Fall schwacher optischer Absorption gilt dagegen:
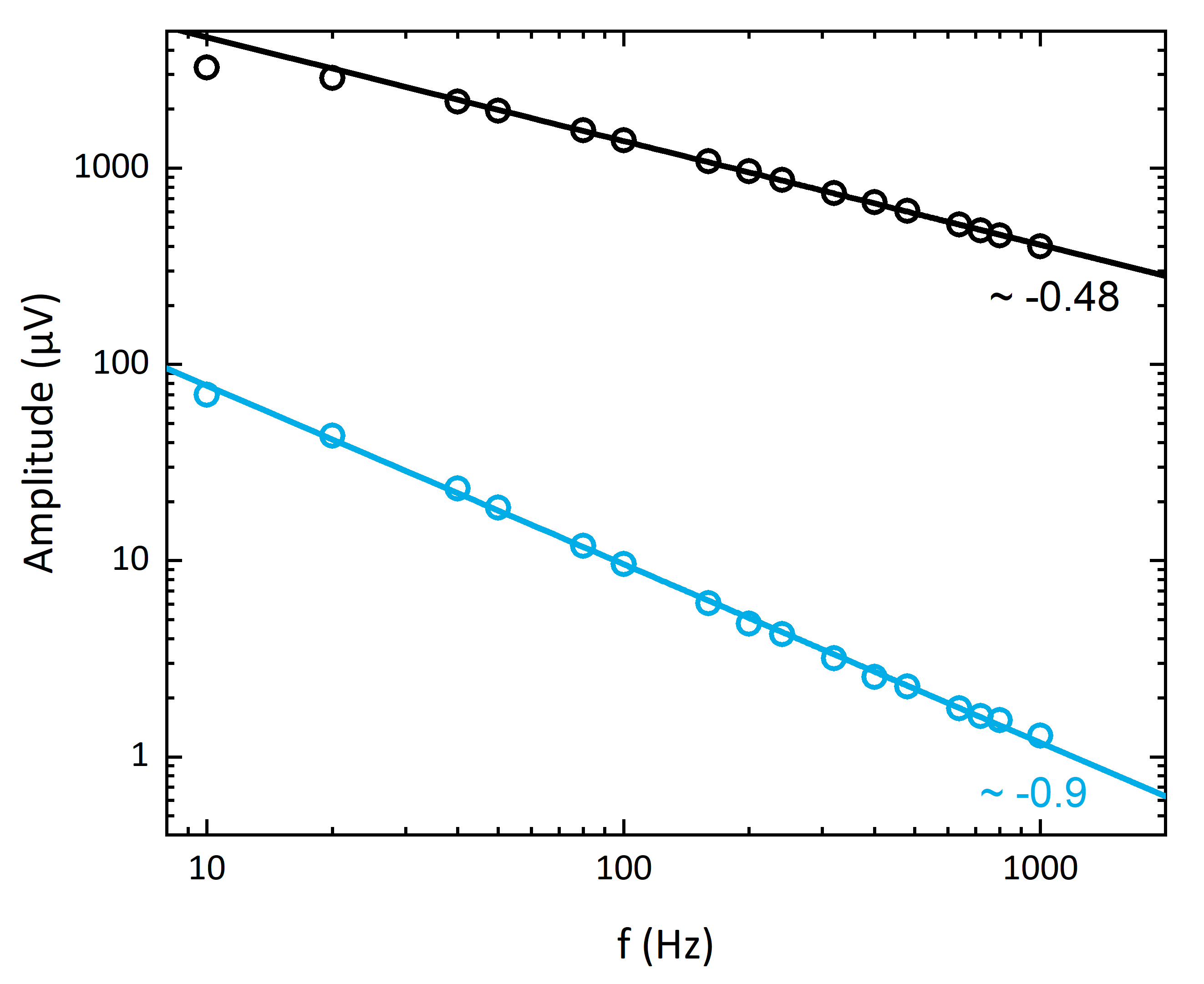
Abb. 5: Verlauf der Amplituden des registrierten Signals für eine Klarlackprobe (blau) mit schlechter optischer Absorption und eine massive Gummiprobe mit hoher optischer Absorption (schwarz). |
Dieses Verhalten lässt sich sehr gut messen, wie Abb. 5 zeigt. Hier sind die Amplituden im Frequenzgang für massives Gummi (schwarze Kreise) und Klarlack (blaue Kreise) gezeigt. Die aus den Gln. (7a, b) erwarteten Exponenten -0,5 für Gummi und -1 für Klarlack lassen sich gut bestätigen. Die Abweichung für Klarlack ist auf das darunterliegende, intransparente Substrat zurückzuführen.
Messbarkeit
Allgemein gilt, dass die Güte photothermischer Messungen, vom Reflexionsvermögen der Oberfläche, vom Absorptionskoeffizienten der Beschichtung und dem Emissionsgrad abhängen. Alle drei Einflüsse sind durch die verwendeten Materialien vorgegeben.
a)
b)
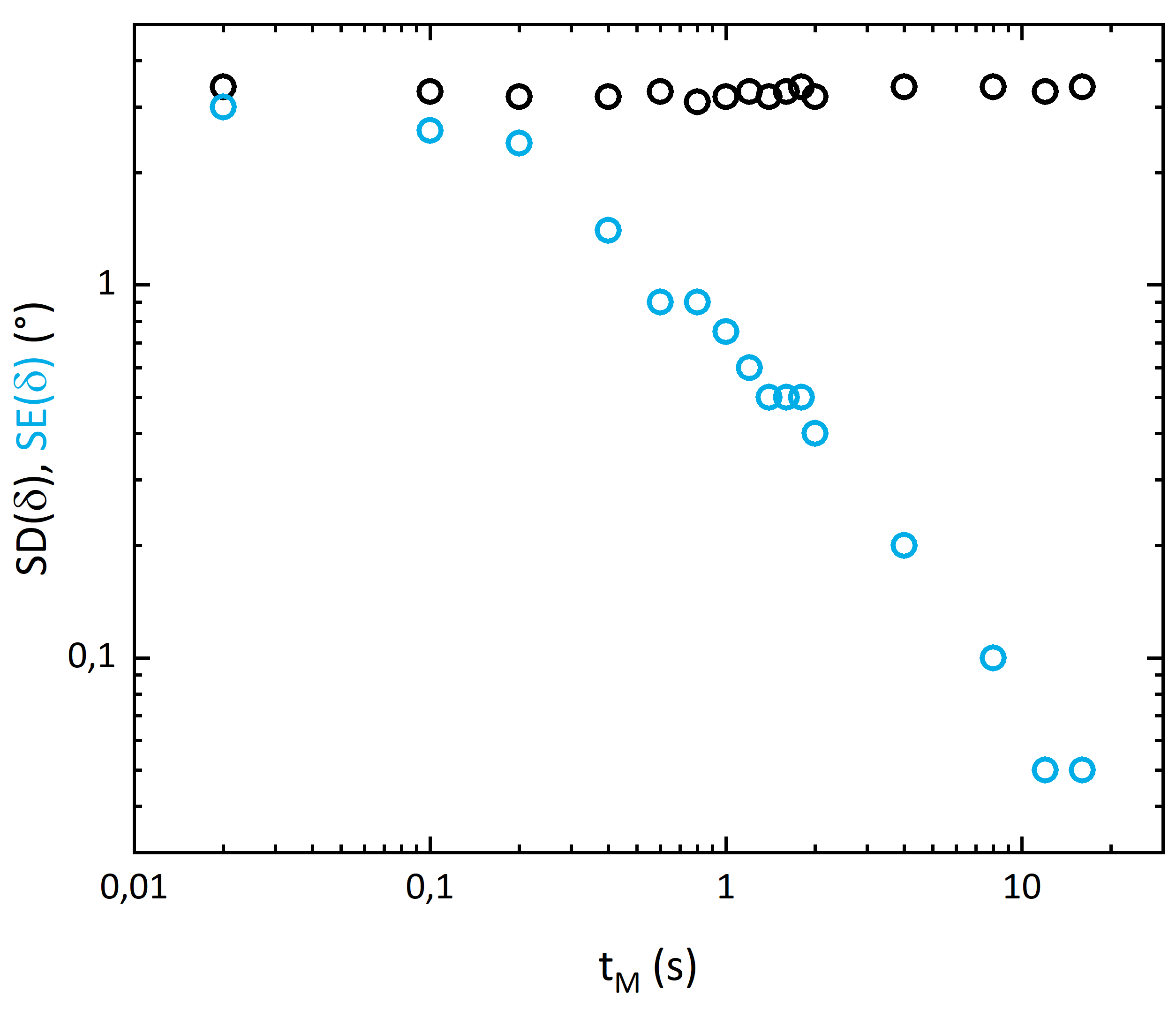
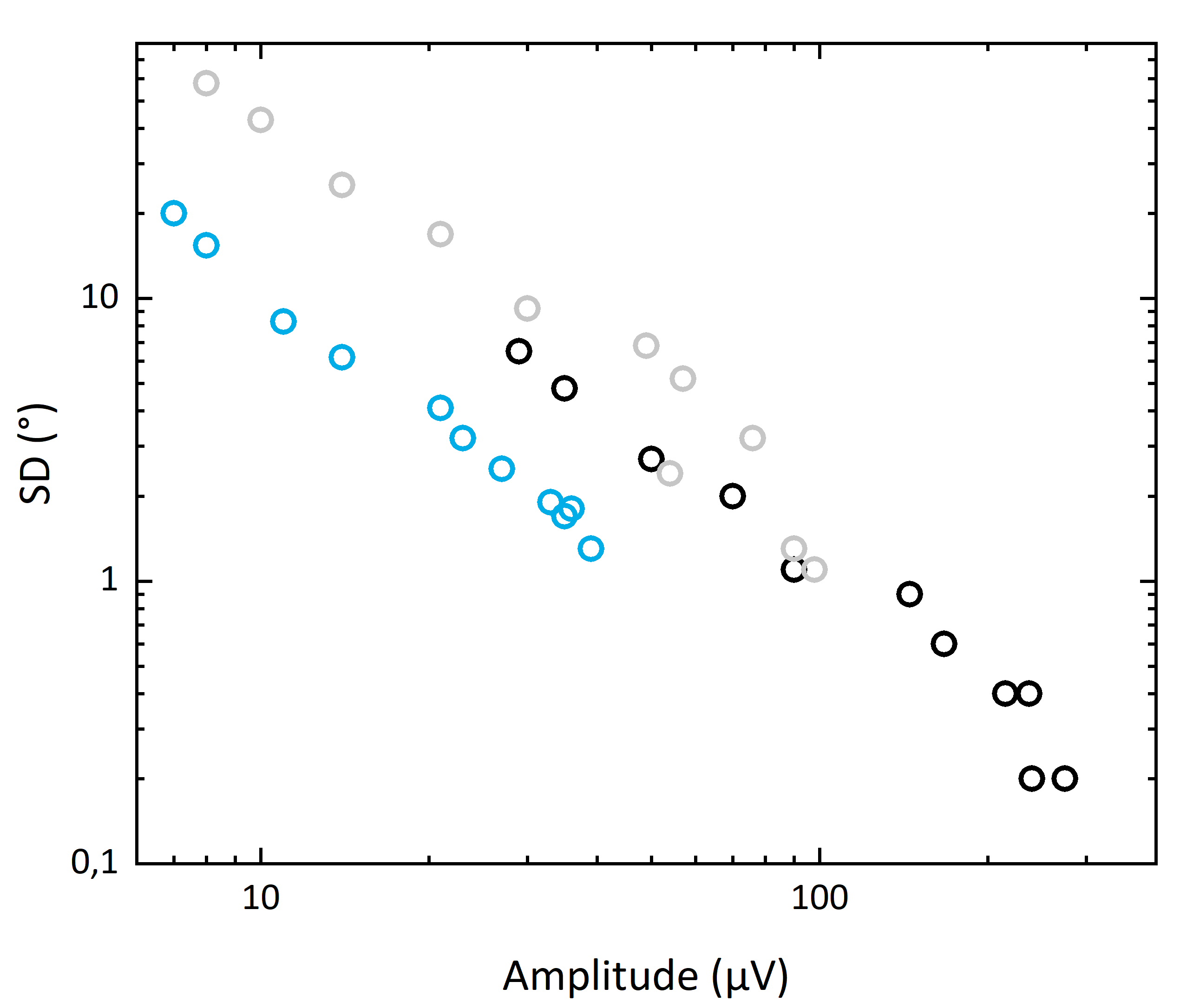
Abb. 6: a) Abhängigkeit der Standardabweichung (der Einzelmessung) von der Amplitude. |
Bei einer periodischen Anregung kann zur Erhöhung der Präzision der Messwert über mehrere Perioden gemittelt werden. Dies ist ein wesentlicher Vorteil gegenüber einer Impulsanregung z.B. mit Blitzlicht. Die Präzision der Messung entspricht dann dem Konfidenzintervall um den Messwert bzw. gemittelten Messwert. Typischerweise wird ein Ein- oder Mehrfaches der Standardabweichung bzw. Standardfehlers als Intervallgrenze herangezogen. Erstere hängt von den Messbedingungen ab. Letzterer kann durch längere Messdauern und damit längere Mittelungszeiten verringert werden [6].
Abbildungen 6a) und b) zeigen diese Zusammenhänge. Für drei Lacke (dunkelgrau, weiß und blau) wird in Abb. 6a) die Abhängigkeit der Standardabweichung der Einzelmessung
von der Amplitude gezeigt. Bei geringen Amplituden sind hier Standardabweichungen von einigen 10° möglich, bis hin
zu weit unter 1° bei hohen Amplituden.
In Abb. 6b) ist für einen weißen Lack gezeigt, wie bei Vergrößerung der Messzeit tM die Standardabweichung der Einzelmessungen zwar konstant bleibt (schwarze Kreise), der Standardfehler jedoch kleiner wird (blaue Kreise). Für einen typischen Basislack liegt der Standardfehler
bereits unter ± 0,2° (0,5 s). Dies entspricht dies einer Präzision von ± 0,2-0,3 µm.
Zusammenfassung
In dieser Application Note haben wir die Voraussetzungen photothermischer Messungen beschrieben und durch Messungen belegt.
Die Qualität photothermischer Messungen hängt vom Absorptionsvermögen des verwendeten Materials, von dessen Emissivität und vom thermooptischen Brechungsindex zwischen Beschichtung und Substrat ab. Photothermische Schichtdickenmessungen eignen sich daher für eine breite Auswahl an Materialsystemen, sofern diese grundlegenden physikalischen Voraussetzungen erfüllt sind.
Auch bei kleiner Signalamplitude kann durch Mittelwertbildung eine hohe Präzision der Messwerte erreicht werden.
Weiterführende Literatur
[1] D. P. Almond and P. M. Patel, Photothermal Science and Techniques, 1st ed. (Chapman & Hall, London, 1996).
[2] W. Macke, Statistik Und Thermodynamik (Akad. Verlagsgs. Geest & Portig, Leipzig, 1962).
[3] A. Rosencwaig and A. Gersho, J. Appl. Phys. 47, 64 (1976).
[4] N. Fernelius, J. Appl. Phys. 51, 650 (1980).
[5] H. Naumann, G. Schröder, and M. Löffler-Mang, Handbuch Bauelemente Der Optik, 7th ed. (Hanser, München, 2014).
[6] H. Kuchling, Taschenbuch Der Physik, 18th ed. (Fachbuchverlag Leipzig, Leipzig, 2004).
Diese Application Note teilen:
Bei Rückfragen stehen wir Ihnen gerne zur Verfügung:
